Khan Academy | Economy | Finance & Capital Market
e & Compound Interest
သင့် အနီးအနားမှာ ငွေတိုး ချေးစားတဲ့သူ ဆီ ငွေချေးတဲ့အခါ ၁နှစ် အတွက် အတိုးနှုန်း ၁၀၀ ရာခိုင်နှုန်း ယူတယ် ဆိုပါစို့။
၁ ကျပ် ချေးတဲ့အတွက် ၁ နှစ်ပြည့်တဲ့အခါ အတိုး ၁ ကျပ် နဲ့ တိုးရင်းပေါင်း (အတိုး+အရင်း) ၂ ကျပ် ပြန်ပေးရမှာ ဖြစ်ပါတယ်။
အကယ်လို့ သင်က ၆ လ အတွက်သာ ချေးပါက အတိုးနှုန်းက ၁၀၀ ရာခိုင်နှုန်း တစ်ဝက် – ၅၀ ရာခိုင်နှုန်း ဖြစ်မှာဖြစ်ပြီး ၆ လကုန်လို့ မဆပ်နိုင်ဘဲ နောက် ၆ လ ထပ်ချေးငှါး ရပါက Compound Interest နည်းဖြင့် တွက်ပါက ၂ ကျပ် ၂၅ ပြား ကျသင့်မှာ ဖြစ်ပါတယ်။
အကြိမ်အရေအတွက်များများ ခွဲတွက်လေလေ
သင်အဖို့ အတိုးများများ ပေးရလေလေ။
ငွေရင်း Principal = p
တစ်နှစ်အတွက် အတိုးနှုန်း = 100%
တစ်နှစ်အတွင်း ခွဲသည့်အကြိမ်အရေအတွက် = n
p [ 1 + ( 100% / n ) ] n
နေ့တိုး ဖြစ်အောင် n = 365 ဖြင့် တွက်ပါက 2.7145675 ရမှာ ဖြစ်ပါတယ်။
အဲ့ဒါက e တန်ဖိုး 2.7182818 နှင့် အနီးစပ်ဆုံး တူညီနေသည် ကို တွေ့ရပါသည်။
e as a limit
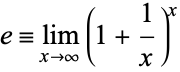
= 2.7182818 ……
ကိန်းဂဏန်း ကြီးလေလေ e တန်ဖိုး ၏ Decimal နေရာ များများ တူလေလေ။
အကယ်၍သာ x = ∞ (Infinity) ဖြစ်ခဲ့ပါက ရလာမယ့်တန်ဖိုးက e အတိအကျသာ ဖြစ်ပေသည်။
e သည်လည်း π (pi) ကဲ့သို့ပင် never repeated decimal value ရှိသော Special ကိန်းဂဏန်း တစ်ခု ဖြစ်သည်။
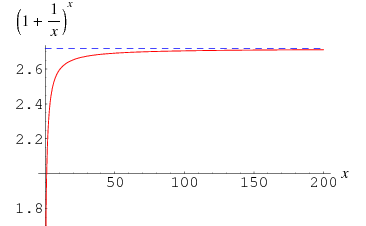
ပထမ ပုံ ကတော့ x တန်ဖိုး 200 နားကပ်သွားရင်တောင် e တန်ဖိုးလောက် ဖြစ်နေပါလိမ့်မည်။
ဒုတိယ ပုံ ကတော့ တွက်လိုက်ရင် ဖြစ်နိုင်တဲ့ နယ်ပယ်ပါ။ Range 1 –> e
If x = 0
y = ( 1 + 1/0)0 = 1
If x = ∞
y = ( 1 + 1/∞)∞ = e
Formula for Continuously Compound Interest
p ( 1 + r/n ) n t
p = Principal
r = Interest Rate in a year
n = ? times in a year
t = ? years
အကယ်၍ n = ∞ သာ ဖြစ်ခဲ့ပါက
p e r t
Euler’s Number (e)

e ဆိုတဲ့ ကိန်းသေဂဏန်း ကို ဆွစ်သင်္ချာပညာရှင် Leonhard Euler ဆိုသူက Exponent ထိပ်စာလုံး e မှည့်ခေါ်ထားတာ။ Exponential growth or decay ဆိုတာ ဆပွါး သို့မဟုတ် ဆလျော့တဲ့ အခြေအနေတွေ တွက်ချက်ရာမှာ သုံးတယ်။
ဘက်တီးရီးယားတွေ ပွါးတာတို့၊ ဗိုင်းရပ်ပိုး ကူးဆက်တာတို့ဆို ဆပွါး ပွါးပါတယ်။ စီးပွားရေး ငွေရေးကြေးရေးတွေမှာတော့ Compount Interest တိုးရင်းပေါင်း အတိုးတွေ တွက်ရင်လည်း ဆပွါး ပွါးတဲ့အတွက်ကြောင့် e ကို သုံး၍ တွက်ရတာမျိုးတွေ ရှိပါတယ်။